Physik und Anwendungen der Mathematik
Im Schwerpunktfach „Physik und Anwendungen der Mathematik“ (PhAM) lernen die Schülerinnen und Schüler wesentliche Grundfertigkeiten des naturwissenschaftlichen Denkens und Arbeitens kennen und in einer Vielzahl von Übungs- und Lernsituationen anwenden.
Sie haben bei uns die Möglichkeit, ihr naturwissenschaftliches Denken zu schulen und Teilgebiete der Mathematik und Physik zu vertiefen. Das so erworbene Wissen und Denken ist insbesondere für ein Ingenieurstudium, Architekturstudium oder ein naturwissenschaftliches Studium generell von grossem Nutzen. Das Fach PhAM wird in drei Einheiten gegliedert: In das Physikpraktikum, den ergänzenden Physik-Theorie-Unterricht und Mathematik, wo besondere Anwendungsgebiete der Mathematik vorgestellt werden.
Im Physikpraktikum steht das experimentelle Arbeiten im Mittelpunkt, d.h. das Gewinnen von Einsicht und Erkenntnis anhand der Naturbeobachtung. Dabei geht es vor allem darum, natürliche Vorgänge durch eigenes Entdecken kennen und möglichst präzis beschreiben zu lernen. Das eigene Erleben des Beobachtens und Experimentierens ermöglicht es den Schülerinnen und Schülern, falsche Vorstellungen und Vorurteile zu klären und in scheinbar zusammenhangslosen oder komplizierten Verhältnissen einfache Zusammenhänge zu erkennen. Sie machen die Erfahrung, dass sie mit ihren Sinnen und ihrem Verstand ihr Umfeld erschliessen und verstehen können, wenn sie bereit sind, sorgfältig wahrzunehmen und ihre Wahrnehmungen sorgfältig auszuwerten. Diese Grundhaltung ist die Basis für jedes wissenschaftliche Arbeiten, nicht nur innerhalb der Physik.
Im Physikunterricht kommen physikalische Phänomene zur Sprache, die über das Grundlagenfach hinausgehen und oft einen themenübergreifenden Charakter haben, z.B. „Erhaltungssätze“ (Energie, Impuls, Drehimpuls), „Gravitation und Planetenbewegungen“ oder „Schwingungen und Wellen“ (Optik, Akustik, Elektrizität). Die Schülerinnen und Schüler lernen dabei, die theoretischen Kenntnisse, die sie im Grundlagenfach erworben haben, in einem komplexeren Kontext anzuwenden und miteinander zu kombinieren. Sie erkennen, dass die gelernten Methoden vielseitig anwendbar und die bereits bekannten Gesetzmässigkeiten grundsätzlich gültig sind. Dadurch entsteht ein physikalisches Verständnis, wie es im Grundlagenfach nicht erreicht werden kann.
In den Anwendungen der Mathematik werden die mathematischen Grundlagen und Fertigkeiten erarbeitet, mit denen die im physikalischen Teil besprochenen Zusammenhänge und Gesetzmässigkeiten quantitativ beschrieben werden können. Dazu gehören z.B. Kegelschnitte (Ellipsen, Hyperbeln und Parabeln), Datenanalyse (Fehlerrechnung, Regression), komplexe Zahlen oder einfache Methoden zur Lösung von Differentialgleichungen. Diese mathematischen Fertigkeiten bilden grundlegende Werkzeuge, die auch im Hinblick auf ein späteres naturwissenschaftliches Studium sehr wertvoll sind.
Stundentafel
|
1. Klasse
|
2. Klasse
|
3. Klasse
|
4. Klasse
|
|
| Schwerpunkt Physik Anwendungen der Mathematik |
1*+2
|
2*+2
|
2*+2
|
3*+2
|
Lesebeispiel: *1 Lektion im Abteilungsunterricht (2 Lektionen 14-täglich in Halbklassen).
Beispiele aus dem Unterricht
Die folgenden Beispiele zeigen exemplarisch einige Themen und Anwendungen, an denen die theoretischen Grundlagen des Unterrichts illustriert, geübt und vertieft werden können.
Bahnkurven von Satelliten und Meteoriten im Anziehungsbereich der Erde
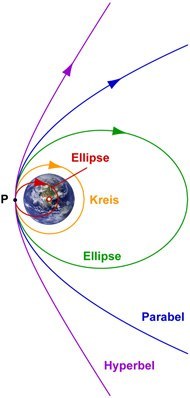
Satelliten oder kleine Himmelskörper, die sich im Anziehungsbereich der Erde befinden, bewegen sich auf Bahnen, die sich mathematisch durch sog. Kegelschnitte beschreiben lassen (Ellipsen, Parabeln oder Hyperbeln, siehe Figur links).
Der Typ des Kegelschnitts wird bestimmt durch die Geschwindigkeit des Objekts im erdnahen Punkt P seiner Bahn. Falls diese Geschwindigkeit
- kleiner ist als die sog. „Kreisbahngeschwindigkeit“, so fällt er auf einer ellipsenförmigen Bahn gegen die Erde,
- gleich gross ist wie die Kreisbahngeschwindigkeit, so bewegt er sich auf einer kreisförmigen Bahn um die Erde,
- grösser ist als die Kreisbahngeschwindigkeit, aber kleiner als die sog. „Fluchtgeschwindigkeit“ (grüner Bereich im Diagramm), so bewegt er sich auf einer ellipsenförmigen Bahn um die Erde.
- gleich gross ist wie die Fluchtgeschwindigkeit, so bewegt er sich auf einer parabelförmigen Bahn von der Erde weg,
- grösser ist als die Fluchtgeschwindigkeit, so bewegt er sich auf einer hyperbelförmigen Bahn von der Erde weg.
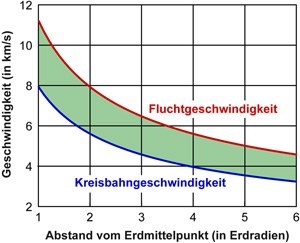
Die Grösse der Kreisbahn- bzw. Fluchtgeschwindigkeit ist selber vom Abstand des Punktes P vom Erdmittelpunkt abhängig (siehe Figur rechts); auf der Erdoberfläche beträgt die Kreisbahngeschwindigkeit rund 7.9 km/s, die Fluchtgeschwindigkeit rund 11.2 km/s.
An diesem Beispiel lernen die Schülerinnen und Schüler,
- die Grundgesetze der Himmelsmechanik kennen, insbesondere die drei Gesetze von Kepler.
- dass sich mathematisch-geometrische Zusammenhänge (zwischen den drei verschiedenen Typen von Kegelschnitten) oft in physikalisch-natürlichen Zusammenhängen (den verschiedenen Typen von Bahnkurven) zeigen.
- dass einfache Gesetze (das Gravitationsgesetz) zu verschiedenen Phänomenen (Bahnkurven) führen können, sich diese aber unter einem gemeinsamen Gesichtspunkt (Kegelschnitte) beschreiben lassen, wenn die Begriffsbildung geeignet abstrahiert wird.
Stromlinien in der Umgebung eines Flügelprofils (Joukowski-Profil)
Die sog. Joukowski-Funktion f:w=1/2·(z+1/z) bildet einen Kreis der komplexen z-Ebene, der durch den Punkt 1 geht und den Punkt –1 im Innern enthält, auf ein sog. Joukowski-Profil ab, das die Form eines Flügelprofils hat. Die Umkehrfunktion f –1: z = w ±(w2–1)0.5 bildet den Einheitskreis der w-Ebene auf das Intervall [-1, 1] der z-Ebene ab. Durch geeignete Kombination beider Abbildungen können Stromlinienbilder in der Umgebung eines Flügelprofils erstellt werden:
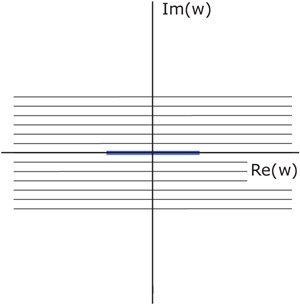
Stromlinien um eine horizontale Platte in der komplexen w-Ebene. Die Platte wird durch das Intervall w ∈ [-1, 1] dargestellt.
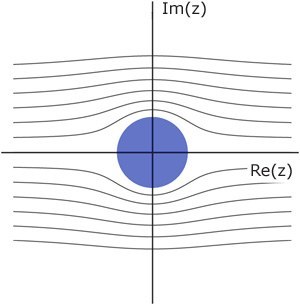
Das Intervall [-1, 1] der w-Ebene wird mit der Relation z = w ± (w2-1)0.5 auf den Einheitskreis der z-Ebene abgebildet. Stromlinien werden auf Stromlinien abgebildet.
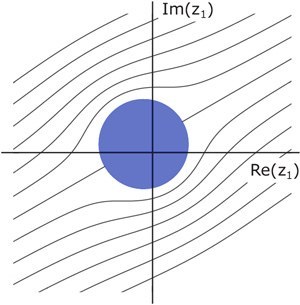
Der Einheitskreis der z-Ebene wird mit der Funktion z1 = r·cis(α)·z + m auf einen Kreis der z1-Ebene abgebildet, der durch den Punkt 1 verläuft und den Mittelpunkt m hat. Zudem wird die ganze z-Ebene um den Winkel α gedreht.
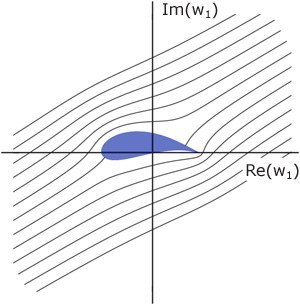
Der Kreis in der z1-Ebene wird mit der Funktion w1 = 0.5 (z1+1/z1) auf ein Flügelprofil abgebildet. Stromlinien werden auf Stromlinien abgebildet.
An diesem Beispiel lernen die Schülerinnen und Schüler,
- den Zusammenhang zwischen komplexen Funktionen und zweidimensionalen Abbildungen zu vertiefen (in der Regel kennen sie zu diesem Zeitpunkt bereits einfachere komplexe Funktionen).
- wie man durch geeignete Kombination einfacher Funktionen komplizierte Abbildungen erzeugen kann.
- komplexere Aufgaben als Abfolge bekannter Teilschritte zu erkennen und zu lösen.
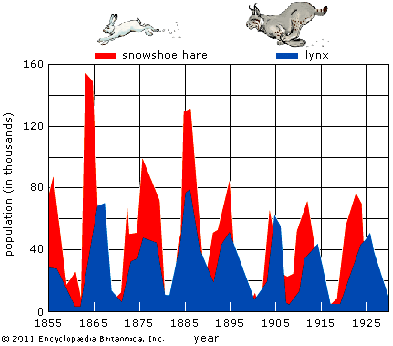
Die nebenstehende Figur zeigt die Populationen von Schneehasen und Luchsen im Gebiet der Hudson Bay (Kanada), empirisch bestimmt aus Daten des Fellhandels.
Die untere Figur zeigt das Resultat einer sog. Modellierung, d.h. einer mathematischen Beschreibung der wesentlichen Grössen und ihrer gegenseitigen Beziehungen:
dH/dt = c1·H-c2·H·LdL/dt = c3·H·L-c4·L
Darin bezeichnen H und L die Anzahl Schneehasen bzw. Luchse im Laufe der Zeit t. Die Zahlenwerte c1, c2, c3 und c4 beschreiben die Sterbe- und Vermehrungsraten der Tiere, c1 und c4 aufgrund von Geburt und natürlichem Tod, c2 und c3 aufgrund von Begegnungen mit der andern Art. Die Differentialquotienten dH/dt und dL/dt bezeichnen die Zu- oder Abnahme der jeweiligen Anzahl pro Zeit.
An diesem Beispiel lernen die Schülerinnen und Schüler,
- die Methode der mathematischen Modellierung kennen. Diese ist in den Naturwissenschaften sowohl für die Beschreibung von Phänomenen als auch für die Vertiefung von Verständnis sehr wertvoll.
- wie man mit Hilfe von gekoppelten Differentialgleichungen komplexe dynamische Systeme beschreiben kann.
- die Funktionsweise von sog. Räuber-Beute-Systemen kennen, insbesondere die Ursache von Zyklizität.
| Typ | Titel | Grösse |
|---|---|---|
| Druckversion | 1.4 MB |

